What Is Cryptography?
Cryptography is the practice and study of techniques for securing communication and information by transforming it into a format that is unreadable to unauthorized users. When sufficient cryptographic measures are in place, even if an unwanted third party did gain access to protected data, they would not be able to decipher it.
This field of science has historically been a source of political contention. During World War II, a British mathematician named Alan Turing, was a key figure in cracking the ENIGMA code. The ENIGMA was a machine used by the German military to send cryptological messages to advance their war effort. Due to this, Turing’s work is credited as a vital component of ending the war. Turing also went on to become one of the major drivers of what would eventually become the modern-day computer we are familiar with today.
Additionally, the creator of Pretty Good Privacy (PGP), Philip Zimmermann was subjected to a criminal investigation headed by the United States Customs Service. PGP, a cryptographic security program that is still widely used to this day, was considered to be too strong of an algorithm for export from the United States. The U.S. government, fearful that its enemies would use PGP, alleged that it violated the Arms Export Control Act – the same law that governs the export of weapons such as machine guns and missile systems. Ultimately, the Massachusetts Institute of Technology (MIT) came to Zimmermann’s aid and published a book that included PGP code to make the point that if he was truly an illegal arms dealer, then so was the university.
Encryption & Decryption
When data is encrypted, human-readable plaintext, such as the sentence you are currently reading, is converted into what is known as ciphertext. Ciphertext is an unreadable, scrambled version of the original plaintext. This is achieved by utilizing mathematical formulas, known as algorithms, that rely on what are referred to as keys. Keys are essentially passwords that are used by cryptographic algorithms to convert plaintext into ciphertext. Keys are also used in the process of reverting ciphertext back into its original plaintext, known as decryption.
As an example, the string “Hello, World!”, when encrypted with the Advanced Encryption Standard with a 256-bit key (AES-256) algorithm, and a key string of “secret” returns the following:
|
eyJpdiI6Ill3THVuSmxvV0hxRG5GZzN0dWxGY0E9PSIsCiJ2Ijox |
There are two major types of encryption.
1. Symmetric-key encryption
Also known as “shared key encryption”, both the sender and receiver share the same key. Just as in the example above, the same key is used for both encryption and decryption.
2. Asymmetric-key encryption
Also known as “public key encryption”, asymmetric-key encryption uses two different keys – a public key and a private key that are mathematically related to each other. Each device involved in communication will have their own public and private key pair.
The public key is distributed by a device to any other device that it wants to communicate securely with, while the private key is kept a secret. The device sending data will encrypt the data with the public key of the recipient device. Once the data is delivered to the recipient, since the private key is mathematically related to the public key, the data can be decrypted with the recipient’s private key.
Cryptographic Failures in Encryption
In general, data is processed by computers in “blocks”. Both symmetric and asymmetric encryption modes operate on fixed block sizes defined by the encryption standard used. For example, the Advanced Encryption Standard (AES) has a block size of 128 bits. Since a byte is 8 bits, in AES-128, data is split in blocks of 16 bytes each.
For example, the string “telecommunicator” is 16 bytes long. By making conversions between encoding schemes equivalents, “telecommunicator” would produce the following block:
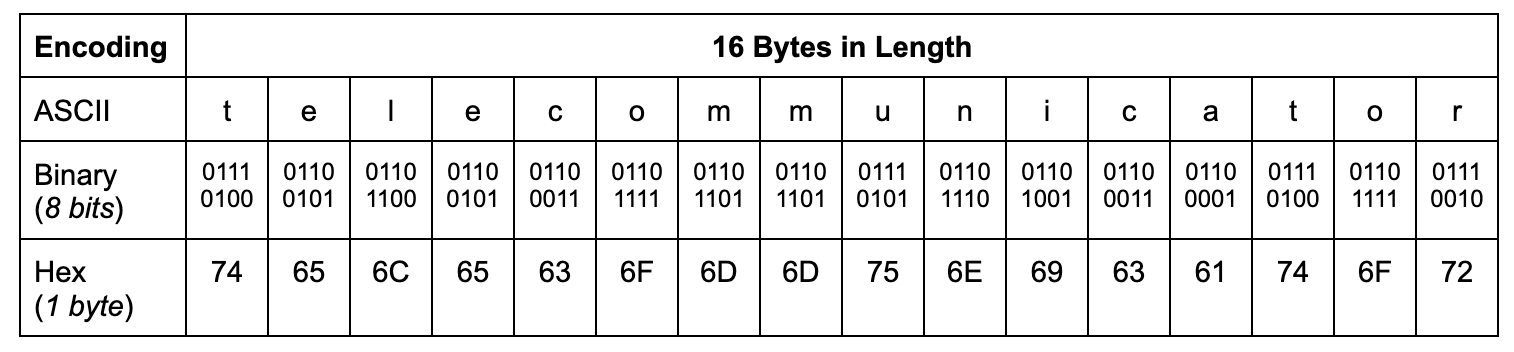
There are different modes used for block encryption. The two that will be covered are ECB and CBC.
Electronic Code Block (ECB)
This mode encrypts every block individually, meaning identical plaintext produces identical ciphertext. You wouldn’t be able to decrypt the ciphertext without knowing the key, but if the ciphertext of two blocks matches, then the plaintext input must match as well.
This creates patterns in the encryption process. This is why the ECB mode is not recommended for use within security contexts. This can be seen visually in images:
Cipher Block Chaining
XOR is a boolean algebra operator that will return true, if and only if exactly one of your input values is true.
This mode solves the issue with ECB by introducing an Initialization Vector (IV) block that is used with the Exclusive OR (⊕) operation on the first block, so that if the first two input values are ever the same, they will produce a different ciphertext output.
Additionally, the ciphertext output of the first block is then used as input to the second block’s XOR operation. Then the ciphertext output of the second block will be used as input to the third block’s XOR operation and so on and so forth – essentially linking the output of one block to the input of the next.
Padding
AES requires blocks to be 16 bytes, so if a block is less than that, there will need to be padding. The preferred padding standard is PKCS #7. In this standard, if you have to pad one byte you pad it with 0x01. If you have to pad two bites you pad it with 0x02 0x02. If you have to pad two bites you pad it with 0x03 0x03 0x03 and so on. Full 16 byte blocks will be followed by a fully padded block.
Padding examples:
|
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
01 |
|
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
02 |
02 |
|
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
03 |
03 |
03 |
Mutating the second to last byte in a block that only has one byte of padding, will not invalidate it (denoted with #):
Padding Oracle Attacks
An oracle in the time of the ancient Greeks was a person or place that could communicate with the gods. In cryptography, a padding oracle is a system that provides information about encrypted data without revealing the encryption key.
Imagine a web server that encrypts cookies before sending them to a client. When the web server receives them back, it will decrypt them in order to process them. Then it will remove the padding. If invalid padding causes an error message or response latency, then you have a padding oracle to work with. For example, a server may send an error message of “AES-128 decryption failed”. This would indicate you exceeded the number of padded bytes.
By modifying the encrypted cookie, you are modifying the ciphertext. By submitting ciphertext to a padding oracle which will either confirm or deny the padding of the plaintext is correct, you can completely decrypt the cookie.
AES CBC Decoding
Since this attack works on one block at a time, we will view the decoding process for a single block:
The decoding process is just the inverse of the encoding process:
- The ciphertext is decrypted using the unknown key on the server.
- The output is an intermediate value known as a key stream.
- The key stream value is then XORed with the IV to produce the plaintext.
This is what the process in its entirety would look like:
But in our case, we don’t know all these values.
After zeroing out the IV, the padding oracle will return a padding error. When a valid value for the 16th byte of the IV is discovered, there will be no padding error.
The plaintext either ends with one 01, two 02s, three 03s, and so on. We can assume the plaintext ends with 01 since valid padding was returned with 1f.
KS16 ⊕ 1f = 01
KS16 ⊕ 1f ⊕ 1f = 01 ⊕ 1f
KS16 ⊕ 00 = 01 ⊕ 1f
KS16 = 01 ⊕ 1f
KS16 =1e
Since the original 16th byte of the IV was 1b:
PT16 = 1e ⊕ 1b
PT16 = 05
We have now determined that the 16th byte of the plaintext value is 05.
Now, we need to set the value of the 16th byte of plaintext to 02. XOR against 1e until you get 02. Set the value to the 16th byte of the IV.
1e ⊕ ? ⊕ = 02
Next, iterate through all the hex values of the 15th byte of the IV, again until the padding oracle doesn’t return an error.
KS15 = c3 ⊕ 02
Since the original 15th byte of the IV was c4:
PT15 = c1 ⊕ c4
PT15 = 05
This checks out because there will be five 05 bytes as padding. This process is repeated until the entire plaintext value that the server receives is discovered.
Try a padding oracle attack yourself here.
PortSwigger Lab: Authentication Bypass Via Encryption Oracle
PortSwigger provides an exercise in their academy in which you have to utilize an encryption oracle. Below are step-by-step instructions on how to solve the lab.
1. Log in using the provided credentials, ensuring to select the ‘Stay logged in’ option.
2. The simulated website is a blogging site in which you can comment on posts. Submitting a comment with an invalid email address results in an error message: “Invalid email address: [email]”
3. In BurpSuite’s HTTP history, select the POST /post/comment request and inspect the response. The server set a ‘notification’ cookie. Inspect the subsequent response to the GET request generated by the 302 redirect. In the header of the HTML file, is a class attribute of “notification-header”. Underneath this is the error message received from submitting an invalid email address.
4. Back in the POST /post/comment request, copy the value of the ‘stay-logged-in’ cookie and paste it as the value of the ‘notification’ cookie in the GET /post?postId=[blog-number], then send the request. Now in the response body, ‘wiener:[timestamp]’. It is now confirmed that the POST request can be used to encrypt data via the email parameter and the GET request can decrypt the data. This will serve as your oracle.
5. Submit ‘administrator:[timestamp]’ as the value of the email parameter. In the response to this request, again copy the value of the ‘notification’ cookie and decrypt it with the GET request. Now the error message is: “Invalid email address: administrator:[timestamp]”.
6. Return to the POST request and send the value of the ‘notification’ cookie to Decoder. Decode as URL and decode as Base64. Since ‘Invalid email address: ‘ is 23 bytes long, remove the first 23 bytes. Reencode the cookie.
7. Once again, decode the cookie using the GET request. You will be met with a 500 server error response. However, there is a verbose decryption error message of: “Input length must be multiple of 16 when decrypting with padded cipher”
8. In the POST request, prefix ‘administrator:[timestamp]’ with 9 bytes to satisfy the 16 byte block requirement. Send the request to get the new value of the ‘notification’ cookie from the response. Send this value back to Decoder, decode it and then delete the first two blocks. Reencode and now use the value in the GET request to decrypt it. You have successfully forged an administrator cookie for use as the value to the ‘stay-logged-in’ cookie.
9. By using this administrator token and deleting the ‘session’ cookie in its entirety as to not conflict with the session state. You are now able to gain unauthorized access to the administrator panel and execute operations with this privileged role.
Hashing
In addition to encryption and decryption, cryptography also encompasses hashing. Hashing is a process that converts data into a fixed-length string, known as a hash digest, that acts as a unique identifier of the original data. Hash digests are used for security measures such as integrity checks, digital signatures, and message authentication. While both encryption and hash functions render data unrecognizable, they differ in a major way – due to the algorithms used, in hashing the process is irreversible. However, the algorithms used will always produce the same output for the same input.
For example, the string “Hello, World!” when hashed using the Message Digest 5 (MD5) algorithm, returns the following hash value:
| 65a8e27d8879283831b664bd8b7f0ad4 |
In hashing, even the slightest variations to an input value result in a completely different output. To demonstrate, examine the hash value of “Hello, world!” (note the lowercase “w”):
| 6cd3556deb0da54bca060b4c39479839 |
Since MD5 uses 128-bit encryption, the number of possible unique combinations is 2128 which amounts to 340,282,366,920,938,463,463,374,607,431,768,211,456.
Cryptographic Failures in Hashing
Though the number of unique combinations provided by MD5 is vast, what are referred to as “collisions” have been discovered. A collision occurs when two different input values produce the same hash digest. A famous probability theory phenomenon known as the Birthday Problem illustrates that there is actually a 50% chance of finding an MD5 collision after 264 operations. MD5 was also once thought to be secure against preimage attacks, meaning that even if someone has the hash digest, they cannot easily work backward to find the original input. Though, weaknesses have been found that allow attackers to reverse-engineer hash digests. These reasons are why MD5 is no longer recommended for use within security contexts.
Rainbow Table Attacks
When you create a password, it is often stored in a database as a hash rather than its plaintext value. This acts as a security measure in the event the database is breached. Again, due to the fact that a hashing algorithm will always produce the same output for the same input, there is a much easier way to discover the corresponding plaintext equivalent than attempting either a collision or a preimage attack, thanks to rainbow tables.
Rainbow tables are precomputed lists of hash digests and their plaintext equivalents. If a database of hashed passwords is obtained, you could simply use a rainbow table or the same hashing algorithm used to generate a large number of hash digests by supplying a wordlist. These output values can then be compared against those in the database until a match is discovered.
Additionally, when compared to dictionary or brute force attacks, rainbow table attacks allow for a higher rate of matching attempts due to the fact that is not subjected to the asynchronous nature of awaiting a response to an HTTP request – rainbow attacks are only limited by the processing power of the device it is carried out on.
There are even websites available, such as CrackStation, where you can supply a hash value, which will be checked against their collection of rainbow tables to find a matching plaintext value. CrackStation currently boasts a 15-billion-entry rainbow table for MD5 and SHA1 hashes as well as a 1.5 billion-entry table for other miscellaneous hash algorithms. However, if a salt is being used, this kind of attack can be thwarted.
Conclusion
As you can see, cryptographic vulnerabilities can be devastating if exploited. Whether they arise due to the use of outdated algorithms or a lack of security configurations – they can lead to consequences such as data breaches, data manipulation, non-compliance, and reputational damage.
In conclusion, the importance of sufficient cryptographic practices cannot be overstated. Organizations must regularly reassess their cryptographic protocols, ensuring they are up-to-date and properly configured. If they do not, malicious attackers will have clear opportunities to exploit them.
